How do Ed5519 keys work?
There are several different implementations of the Ed25519 signature system, and they each use slightly different key formats. While writing python-ed25519, I wanted to validate it against the upstream known-answer-tests, so I had to figure out how to convert those keys into a format that my code could use.
The best reference is the original paper, which explains everything you need to know to implement the basic algorithm. I currently know of three or four implementations (many of which are on the Ed25519 software page):
- a portable C “reference” version
- a 10x faster AMD64-optimized C/assembly version (in two flavors, with different speed/memory tradeoffs)
- an educational (but unusably slow) pure-python module
- my Python binding to the C reference version
djb’s NaCl library (as of version 20110221) includes an older copy prototype of the portable C version, in nacl-20110221/crypto_sign/edwards5519sha512batch/ref/ (as far as I can tell, it doesn’t implement quite the same algorithm: it doesn’t include the pubkey in the hash when computing S. UPDATE: djb told me that nacl-20110221’s code is just a prototype, and will be replaced with the real Ed25519 in the next release). The SUPERCOP benchmark suite includes both the portable C and the two AMD64-specific flavors (in supercop-20110704/crypto_sign/ed25519/, under the ref, amd64-51-30k, and amd64-64-24k subdirectories). The pedagogical pure-python implementation is referenced by the ed25519 web page, but since it takes tens of seconds to compute each signature, it’s really only useful for validating the output of other implementations.
My python-ed25519 library provides Python bindings to the portable C version, using code taken from the SUPERCOP suite.
These different implementations all arrange the keys and signatures slightly differently. NaCl’s goal is to provide safe high-level box/unbox functions, so the only interface it offers will copy the entire message into the output and append a signature to it (not so convenient for building into other protocols). SUPERCOP’s goal is to measure the speed of each operation, so its interface isn’t so convenient for general use either. I’ve tried to give python-ed25519 a good interface for use in other projects.
To remind myself about how these different implementations handle keys, here’s an overview.
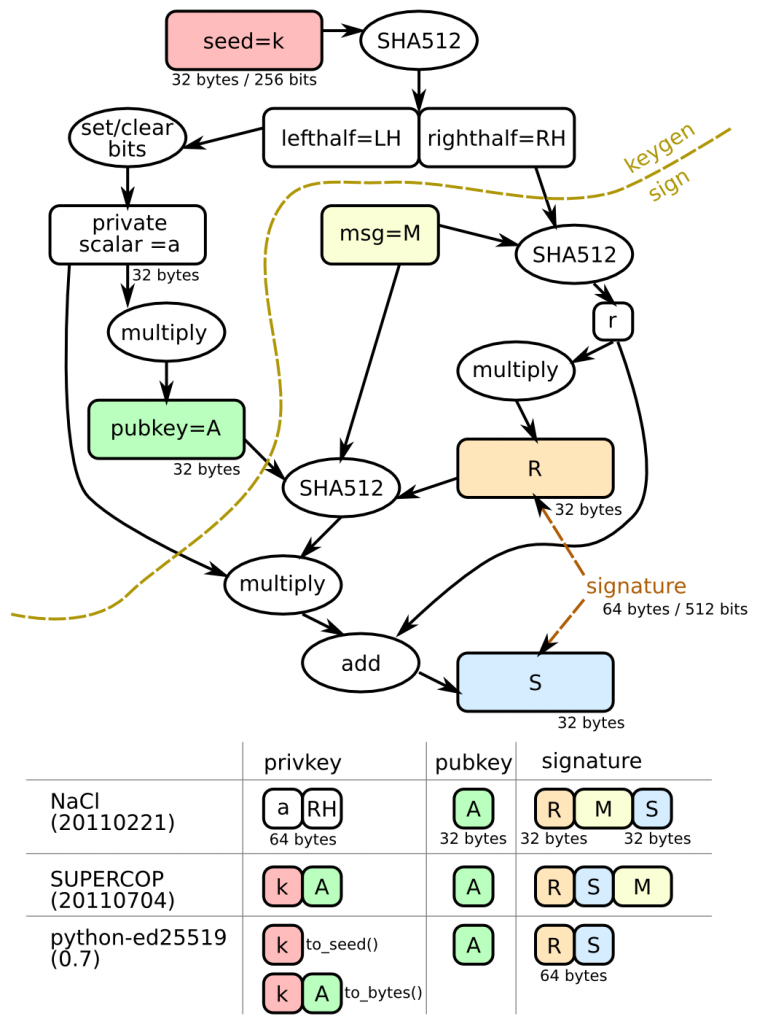
Ed25519 keys start life as a 32-byte (256-bit) uniformly random binary seed (e.g. the output of SHA256 on some random input). The seed is then hashed using SHA512, which gets you 64 bytes (512 bits), which is then split into a “left half” (the first 32 bytes) and a “right half”. The left half is massaged into a curve25519 private scalar “a” by setting and clearing a few high/low-order bits. The pubkey is generated by multiplying this secret scalar by “B” (the generator), which yields a 32-byte/256-bit group element “A”.
When signatures are made, two values result: R and S (both 32-bytes, so the overall signature is 64 bytes long). R depends upon the right half of the expanded seed and on the message. (In traditional DSA, R is randomly generated, and the security of the private key depends upon the quality of that randomness, leading to some high-profile failures). S is the real meat of the signature, and is a function of everything (including the pubkey).
Private signing keys can be generated from just the 32-byte seed, but require additional work before you can make signatures (SHA512-based expansion, the bit setting/clearing massage step, and pubkey exponentiation). Likewise public verifying keys can be derived from either the private seed or the private exponent. (note that it’s the multiplications that take the most time: everything else is trivial by comparison).
If you care more about the speed of operations than storage space, you’d want to store the expanded versions. Or, you might want to store as little information as possible, and accept the performance penalty of re-deriving things when necessary. Different implementations choose different tradeoffs.
With that background, here’s what the different implementations do:
- slow pure-python “ed25519.py” implementation, with Known-Answer-Tests in sign.py and sign.input:
- publickey(sk) takes the seed, returns the 32-byte pubkey
- signature() takes the message to be signed, the seed, and the pubkey, returns the 64-byte signature
- checkvalid() takes the signature, the message, and the 32-byte pubkey
- each line of the test data contains four fields (joined by colons):
- seed+pubkey (64 bytes)
- just the pubkey (32 bytes)
- the message (variable length)
- the signature concatenated with the message (R+S+msg)
- NaCl-20110221 implementation:
- keypair() returns two values. The first (signing key) is the private scalar (32 bytes) concatenated with the “right half” (also 32 bytes). The second is the pubkey (32 bytes)
- sign() takes the signing key and message. The NaCl version doesn’t take the pubkey, and thus diverges from the ed25519.py implementation: S=H(r+msg), not H(r+pubkey+msg). ed25519.py matches the paper, as does SUPERCOP, but NaCl does not. sign() returns R+msg+S
- SUPERCOP-20110704 implementation:
- keypair() returns two values. The first (signing key) is the seed (32 bytes) concatenated with the generated pubkey (32 bytes). The second is the pubkey (32 bytes).
- sign() returns R+S+msg
- python-ed25519 (using the SUPERCOP code but changing the output):
- ed25519.create_keypair() returns a SigningKey object and a VerifyingKey object
- SigningKeys can be serialized with to_bytes() (which returns the same 64 bytes as the SUPERCOP code that it wraps: the seed concatenated with the pubkey A), or with to_seed() (which returns just the 32-byte seed).
- VerifyingKeys can be serialized with to_bytes(), which returns the
32-byte pubkey A. - sk.sign() returns a 64-byte signature (the concatenation of R and S) without returning a copy of the message too. (internally, this invokes SUPERCOP’s crypto_sign() function with an output buffer large enough to hold R+S+msg, then discards the message).
This is summarized in the following diagram:
Have you considered including the ability to recover the public key from a signature, in python-ed25519? The operation is described in the “SEC 1: Elliptic Curve Cryptography” paper, section 4.1.6: http://www.secg.org/download/aid-780/sec1-v2.pdf
This could be really useful for bandwidth-constrained applications, for example in Bitcoin-like blockchains, where every byte is fairly expensive to store.
That’d be kinda neat. I don’t think it’s possible for Ed25519, though, since S involves the hash of the pubkey (along with R and the hash of the message). This breaks the “compute e from M” step (1.5), because you need the candidate public key *first* to make that computation.
http://crypto.stackexchange.com/questions/9936/what-signature-schemes-allow-recovering-the-public-key-from-a-signature has some good discussion.
It’s also not clear to me that you could use such a feature safely. I don’t entirely get the arguments in that paper: any certificate chain *must* uniquely identify the next key being certified, so you can’t afford to leave the key out of the cert. And once you’ve got a copy of the key from there, you don’t need to recover it from other messages.
In my protocols, I include a copy of the key with every message, since it’s pretty short. The verifier starts by checking the signature, then strips it and sends an event “upwards” that includes a tuple of (pubkey, message), and the higher-level software can switch on the pubkey as it sees fit (maybe looking it up in a pre-established table of known identities, maybe allocating a new table entry to this key and treating as a pseudonym).
One conceivable utility for public-key recovery would be if you have a large list of pre-established “acceptable” public keys, and a message arrives which you think is probably signed by a key on that list. Recovery (which, according to the paper, yields a *set* of keys) could narrow down the candidates to a small number, which you then intersect with your acceptable-keys list, then you perform trial verification with all of them until you find one that works.
But, depending upon the size of the list, you could accomplish something comparable by including just a few bits of the pubkey along with the message: enough to reduce the search space to a reasonable value. I call this kind of thing a “key hint”. There’s an obvious tradeoff between size of the list, size of the hint, and the number of trial verifications you have to do.
I tend to think of three kinds of key-identifying values:
* “public-key”: everything necessary to verify a signature
* “key-id”: enough to uniquely+securely identify a public-key, e.g. a fingerprint or hash of the full pubkey. Given a key-id, you can’t necessarily obtain the pubkey. But given a key-id and a purported pubkey, you can confidently say “yes” or “no”.
* “key-hint”: something which narrows down the set of possible pubkeys, but is not enough to safely identify one. Given a key-hint, you could easily make up new keypairs which match.
For RSA, where “public-key” is large (kilobits), we tend to assume that the pubkey will be given to the recipient out-of-band in some kind of ceremony (and generating them is difficult enough that we tend to assume a “one key per human” model, leading to a very identity-centric system). Most certificates include key-ids. Nothing really uses key-hints because the protocols tend to have human- or server- identifiers in them (domain names, email addresses) which then get mapped to the full key by the recipient.
But with ECDSA, everything is so short that all three values can be the same, and it becomes possible to think about one-key-per-program, or even one-key-per-object, and it’s usually feasible to include the whole key with every message. Makes the protocols a *lot* simpler too.
Thanks for your detailed reply.
The protocol for which I plan to use this does narrow down the list of possible public keys significantly. The way it would work is that a specially formatted transaction that we could call a “merchant registration message” is put into the blockchain that contains the public key of this merchant (as an OP_RETURN output (which can be used to include arbitrary data in a Bitcoin transaction)), and an amount of bitcoins that are destroyed (to prevent an excessive number of registrations). This establishes a merchant with a certain public key.
The other type of special transaction (that is put into the blockchain) is an “order message” (the protocol I’m trying to create is that of a decentralized marketplace), which includes a signature over the transaction itself (again in an OP_RETURN output), in order to establish who the merchant is for this order. This way, everyone can scan the blockchain and see how many open/pending orders exist for a certain identity (merchant).
So the number of possible public keys for the signature (in the “order message”) in question is limited to the public keys contained in the “registration messages”, and each client will decide for themselves what the adequate “burn amount” (amount of bitcoins destroyed in the registration message) is, in order to prevent a DoS attack through an excessive number of registrations.
But the whole point is sort of moot anyway, since Bitcoin transactions with an OP_RETURN output are only forwarded by the original Bitcoin client if they include no more than 40 bytes of data or less. But 64 bytes of data is certainly better than 64+32 bytes of data, in any case. The limit was previously 80 bytes – enough to include a signature but not a signature plus public key. So if the limit is ever raised back to 80 bytes, this protocol would only work if the public key can be derived from the signature.
Mind you, it’s certainly possible to split the signature in two, and include the second part in separate transaction, which references the first one, but the Bitcoin developers don’t like that – and I can understand why – so I would really prefer to keep it as clean as possible.
Thinking about this some more, using your concept of a “key-id”, it would be trivial to add a unique ID in each registration message. Then each merchant would have a public key and a unique ID associated with it. Then the order messages can just reference this ID, and clients know which public key to use when verifying a signature. Although this would introduce the problem of how to handle ID collisions.
Anyway, I’m just thinking out loud. Thanks for your answer :).