Telemetry is a feature in Firefox that captures performance metrics such as start up time, DNS latency among others. The number of metrics captured is in the order of a couple hundred. The data is sent back to the Mozilla Bagheera servers which is then analyzed by the engineers.
The Telemetry feature asks the Nightly/Aurora (pre-release) users if they would like to submit their anonymized performance data . This resulted in a response rate (number of people who opted in divided by the number of people who were asked) of less than 3%. This led to two concerns: small number of responses (which changed when Telemetry became part of Firefox release) and more importantly representativeness: are the performance measurements as collected from the 3% representative of those of people who chose not to opt in?
Measuring the bias is not easy unless we have measurements about the users who did not opt in. Firefox sends the following pieces of information to the Mozilla servers: operating system, Firefox version, extension identifiers and the time for the session to be restored. This is sent by all Firefox installations unless the distribution or user have the feature turned off (this is called the services AMO ping). The Telemetry data contains the same pieces of information.
What this implies is that we have start up times for i) the users who opted in to Telemetry and ii) everyone. We can now answer the question “Are the startup times for the people who opted into Telemetry representative of the typical Firefox user?”
Note: ‘everyone’ is almost everyone. Very few have this feature turned off.
Data Collection
We collected start up times for Firefox 7,8 and 9 for November, 2011 from the log files of services.addons.mozilla.org (SAMO). We also took the same information for the same period from the Telemetry data contained in HBase ( some code examples can be found at the end of the article).
Objective
Are start up times different by Firefox version and/or Source, where source can be SAMO or Telemetry.
Displays
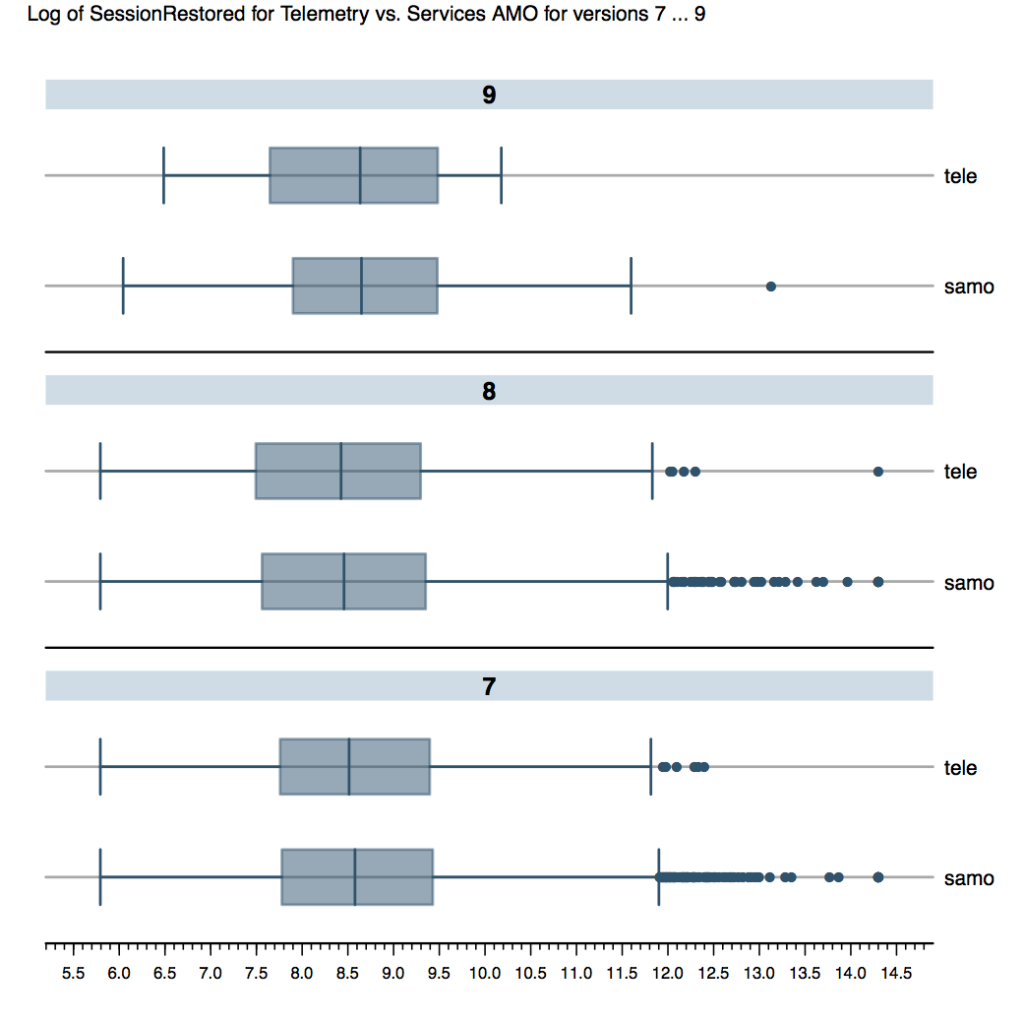
Figure 1 is boxplot of log of start up time for Telemetry (tele) vs. SAMO (samo) by Firefox version. At first glance it appears the start up times from Telemetry are less than those of SAMO. But the length of the bars makes it difficult to stand by this conclusion.
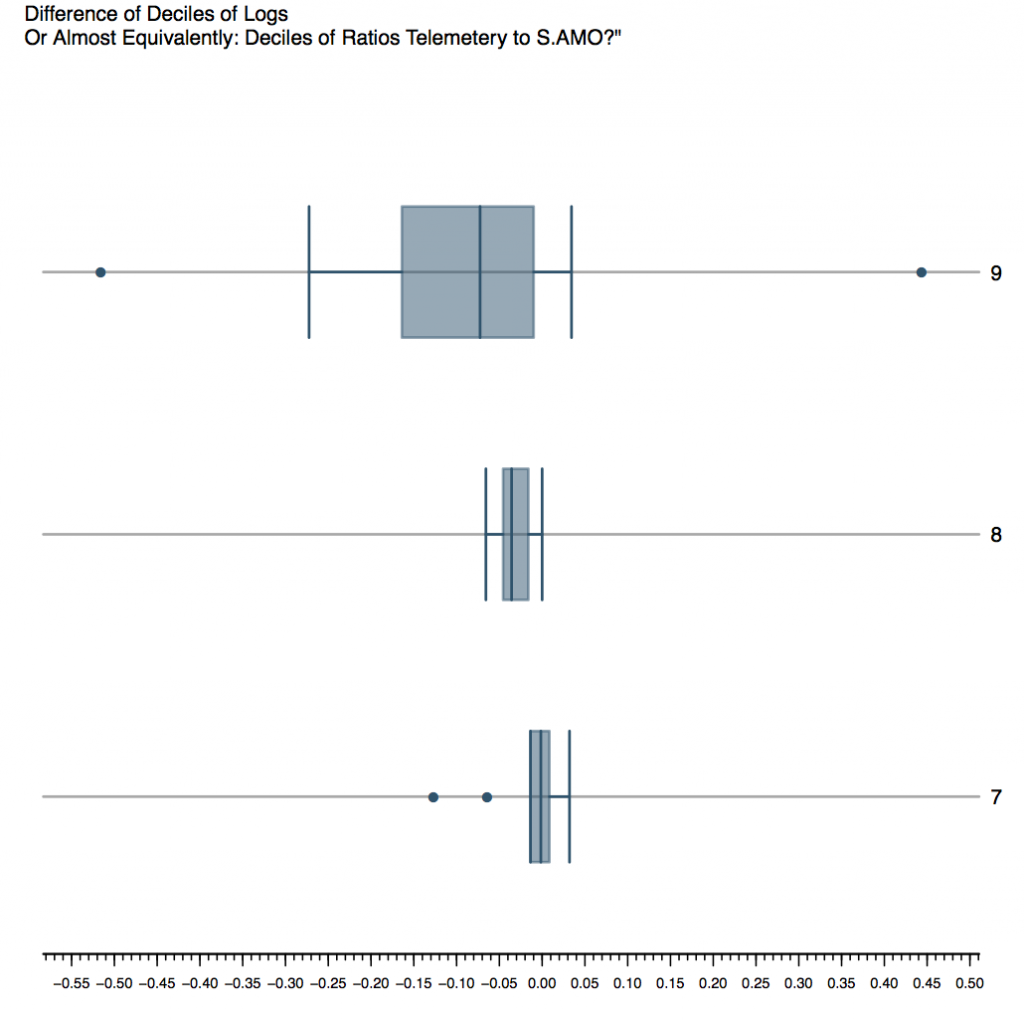
Figure 2 is the difference in the deciles of log of start up time. In other words, approximately speaking, the deciles of ratio of Telemetry start up time to SAMO start up time. The medians hover in the 0.8 region, though the bars are very wide and do not support to a the quick conclusion that Telemetry start up time is smaller.
In Figure 3, we have the mean of medians of 1000 samples: red circles are for telemetry and black for SAMO. The ends of the line segments correspond the sample 95% confidence interval (based on the sample of sample medians). The CI for the SAMO data lies entirely within that of the Telemetry data. This makes one believe that the two groups are not different.
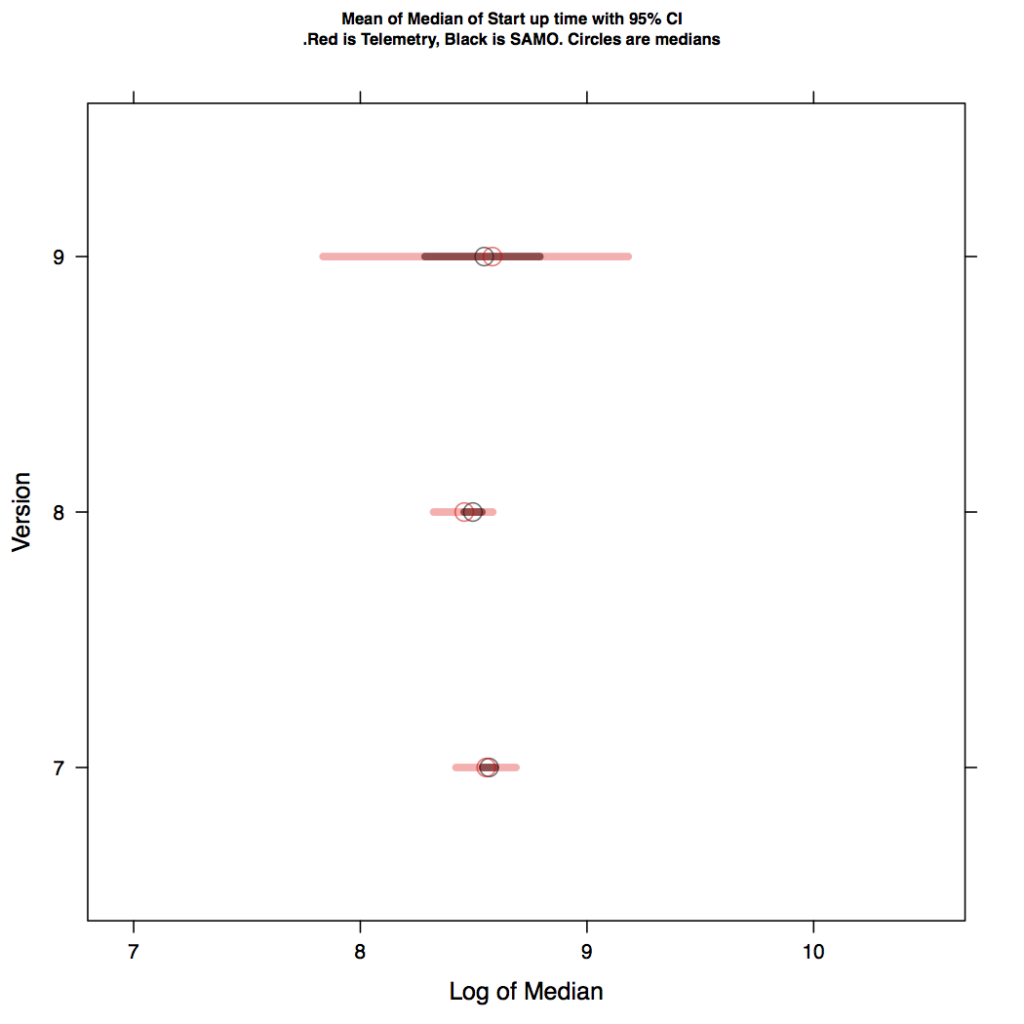
Figure 4: Mean of the medians (circles) with their 95% confidence intervals. Red isTelemetry, Black is SAMO
Analysis of Variance
For a more numerical approach, we can estimate the analayis of variance components. The model is
log(startup time) ~ version + src
(we ignore interaction). Since the data is in the order of billions of rows, I instead take 1000 samples of approximately 20,000 (sampling rate of 0.001%) rows each. Compute ANOVA results of each and then average the summary tables of the lm function in R. In other words we make our conclusions based on the average of the 1000 samples of ~20,000 rows each. ( I should point out that the residuals (as per a quick visual check) were roughly distributed as gaussian and other diagnostics came out clean)
The average ANOVA indicates does not support version effect or source effect (at the 1% level). In other words, the log of start up time is not affected by the version nor is it affected by the source (Telemetry/ SAMO).
Estimate Std. Error t value Pr(>|t|) (Intercept) 8.62635472 0.01171420 736.4390937 0.00000000 vers8 -0.05995627 0.01928947 -3.1089666 0.02922402 vers9 -0.03382135 0.10466330 -0.3247165 0.48286903 vers10 -0.03862282 0.29308642 -0.1418623 0.48228122 srctele -0.02290538 0.03946150 -0.5811779 0.45300964
This is good news! Insofar start up time is concerned, Telemetry is representative of SAMO.
A Different Approach and Some Checks
By now, the reader should note that we have answered our question (see last line of previous section). Two questions remain:
1. The samples are representative. We are sampling on 3 dimensions: startup time, src and version. Consider the 1000 quantiles of startup time, the 2 levels of src and 4 levels of version. All in all, we have 1000x2x4 or 8000 cells. Sampling from the population might result in several empty cells, so much so, that the joint distribution of the sample might be very different from that of the population. To confirm that our cell distribution of the samples reflect the cell distribution of the population, we computed Chi Square tests comparing the sample cell counts with that of the parent. All 1000 samples passed!
2. Why use samples? We can do a log linear regression testing on the 8000 cell counts (i.e all the 1.9 BN data points) . This of course loses a lot of power: we are binning the data and all monotonic transformations are equivalent. The model equivalent (using R’s formula language) of the ANOVA described above is
log(cell count) ~ src+ver+binned_startup:(src+ver)
If the effects of binned_startup:src and binned_startup:ver are not significant this corresponds to our conclusion in the previous section. And nicely enough, it does! Output of summary(aov(glm(…))) is
summary(aov(glmout <- glm(n~ver+src+sesscut:(ver+src)
, family=poisson
, data=cells3.parent))
Df Sum Sq Mean Sq F value Pr(>F) ver 3 4.6465e+14 1.5488e+14 1131.8666 <2e-16 *** src 1 3.2705e+14 3.2705e+14 2390.0704 <2e-16 *** ver:sesscut 3952 5.4969e+13 1.3909e+10 0.1016 1 src:sesscut 988 2.0009e+13 2.0252e+10 0.1480 1 Residuals 2967 4.0600e+14 1.3684e+11
Some R Code and Data Sizes:
1. The data for SAMO was obtained from Hive, sent to a text file and then imported to blocked R data frames using RHIPE. All subsequent analysis was done using RHIPE.
2. The data for Telemetry, was obtained from Hbase using Pig (RHIPE can read HBase, but I couldn’t install it on this particular cluster). The text data was then imported as blocked R data frames and placed in the same directory as the
imported SAMO data.
3. Data sizes were in the few hundreds of gigabytes. All computations were done using RHIPE (R not on the on the nodes) on a 350TB/33 node Hadoop cluster.
3. I include some sample code to give a flavor of RHIPE.
Importing text data as Data Frames
map <- expression({
ln <- strsplit(unlist(map.values),"\001")
a <- do.call("rbind",ln)
addonping <- data.frame(ds=a[,1]
,vers=a[,3]
,sesssionrestored=as.numeric(a[,6])
,src=rep("samo",length(a[,6]))
,stringsAsFactors=FALSE)
rhcollect(runif(1),addonping)
})
z <- rhmr(map=map
,ifolder="/user/sguha/somequants"
,ofolder="/user/sguha/teledf/samo"
,zips="/user/sguha/Rfolder.tar.gz"
,inout=c("text","seq")
,mapred=list(mapred.reduce.tasks=120
,rhipe_map_buff_size=5000))
rhstatus(rhex(z,async=TRUE),mon.sec=4)
Creating Random Samples
map <- expression({
y <- do.call('rbind', map.values)
p <- 20000/1923725302
for(i in 1:1000){
zz <- runif(nrow(y)) < p
mu <- y[zz,,drop=FALSE]
if(nrow(mu)>0)
rhcollect(i,mu)
}
})
reduce <- expression(
pre={ x <- NULL}
,reduce = {
x <- rbind(x,do.call('rbind',reduce.values))
}
,post={ rhcollect(reduce.key,x) }
)
z <- rhmr(map=map,reduce=reduce
,ifolder="/user/sguha/teledfsubs/p*"
,ofolder="/user/sguha/televers/dfsample"
,inout=c('seq','seq')
,orderby='integer'
,partition=list(lims=1,type='integer')
,zips="/user/sguha/Rfolder.tar.gz"
,mapred=list(mapred.reduce.tasks=72
,rhipe_map_buff_size=20))
rhstatus(rhex(z,async=TRUE),mon.sec=5)
Run Models Across Samples
map <- expression({
cuts <- unserialize(charToRaw(Sys.getenv("mcuts")))
lapply(map.values, function(y){
y$tval <- sapply(y$sesssionrestored
,function(r) {
if(is.na(r)) return( r)
max(min(r,cuts[2]),cuts[1])
})
mdl <- lm(log(tval)~vers+src,data=y)
rhcollect(NULL, summary(mdl))
})})
z <- rhmr(map=map
,ifolder="/user/sguha/televers/dfsample/p*"
,ofolder="/user/sguha/televers2",
,zips="/user/sguha/Rfolder.tar.gz"
,inout=c("seq","seq")
,mapred=list(mapred.reduce.tasks=0))
rhstatus(rhex(z,async=TRUE),mon.sec=4)
Computing Cell Counts For A Log Linear Model
cuts2 <- wtd.quantile(tms$x,tms$n,
p=seq(0,1,length=1000))
cuts2[1] <- cuts[1]
cuts2[length(cuts2)] <- cuts[2]
map.count <- expression({
cuts <- unserialize(charToRaw(Sys.getenv("mcuts")))
z <- do.call(rbind,map.values)
z$tval <- sapply(z$sesssionrestored,function(r)
max(min(r,cuts[length(cuts)]),cuts[1]))
z$sessCuts <-
factor(findInterval(z$tval,
cuts),ordered=TRUE)
f <- split(z,list(z$vers,z$sessCuts,z$src),drop=FALSE)
for(i in seq_along(f)){
y <-strsplit(names(f)[[i]],"\\.")[[1]]
rhcollect(y,nrow(f[[i]])) }
})
z <-
rhmr(map=map.count,reduce=rhoptions()$templates$scalarsummer
,combiner=TRUE,
ifolder="/user/sguha/teledfsubs/p*"
,ofolder="/user/sguha/telecells",
,zips="/user/sguha/Rfolder.tar.gz"
,inout=c("seq","seq") ,mapred=
list(mapred.task.timeout=0
,rhipe_map_buff_size=40
,mcuts=rawToChar(serialize(cuts2, NULL,
ascii=TRUE))))
engineering videos wrote on
:
wrote on
: