We’ve previously talked about search engine marketing as one of the key marketing efforts here at Mozilla.  Those previous analyses have pointed to experiments we’ve performed that helped increase our efficiency by approximately 50% earlier this year (that’s pairing a reduction in total spend with an increase in total clicks).  While those are some great gains, we’re always considering additional ways to improve our efficiency, and ultimately the new user’s experience, through this marketing channel.

An example of a potentially untapped area for improvement is day/time parting, i.e., better targeting by day of week or hour of day.  Intuitively, it’s easy to imagine that a particular day (e.g., Fridays) or a particular hour (11pm PT) might see a lower price (cost per click) or differing interest among new users (click through rate).

Fortunately, this is a fairly easy hypothesis to test thanks to regression analysis.  With our AdWords account, we can grab hourly data and see what variables (e.g., particular hours of the day) cause the price/interest changes mentioned above.  Continuing our example, perhaps most advertisers run out of their daily ad budget by the end of day, causing late night hours to see a lessened competitive bidding environment, and consequently, a cheaper cost per click.  Regression analysis would be able to tell us exactly that – and tell us that perhaps we should be diverting more resources to such market inefficiencies.

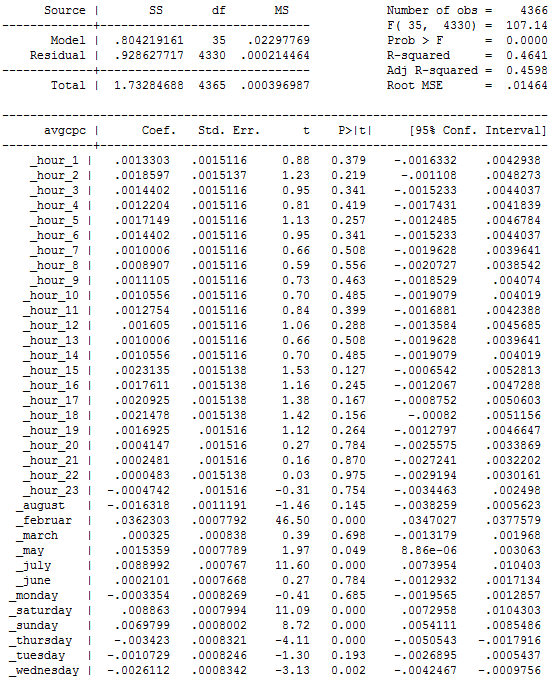
Below is the regression equation and full regression output.  We used a recent data set from our primary campaign containing more than 4,300 hours, which equates to about six months worth of data.  Clearly our equation could be strengthened in different ways (more instances, more control variables).  For example, the results did improve when we substituted the day of week and month variables with a dayofweek*month interaction variable.  For any stats fans reading this, we’re open to other suggestions for improving our work (comments encouraged).

Cost per Click = α + β₁hour_of_day + β₂day_of_week + β₃month + ε

Note: hour of day results are relative to the midnight to 1am hour (pacific time), day of week results are relative to Fridays, and month results are relative to April.

So, how do we interpret these results?

• For hour of day, it looks like there’s little inefficiency to be found.
• However, the day of week findings are generally very robust.  Tuesdays, Wednesdays and Thursdays are relatively less expensive, and Saturdays and Sundays are relatively more expensive.
• At a macro level, these findings tend to point to a generally efficient market, meaning we likely won’t be changing our marketing decision making based on this information alone.